This is the second post of the Introduction to Abstract Algebra series. In the first post, we introduce the basic concepts of groups. In this post, we will introduce four isomorphism theorems. But first of all, we need to define normal groups.

Normal Groups and Quotient Groups

Recall that we define the cosets as the following: Given a group $G, H \subset G$ is a subgroup, for any $g\in G$, $gH$ a left coset of $G$, and $Hg$ is a right coset. We’ve already shown that all the cosets have the same cardinality (by defining an isomorphism). We’ve also shown that the set of left cosets forms a partition of the group. The idea of quotient groups, denoted as $G/H$ is motivated by the following question: can we define a group based on this set, or can we define a proper binary operation $\circ: G/H \times G/H \to G/H$ for this set? A perhaps natural binary operation is $g_1H \circ g_2H = (g_1 g_2)H$. This definition is very convenient, as it has the identity $eH$, an inverse for each element as $gH \circ g^{-1}H = eH$, and satisfies associativity. But it has one significant problem: it may not be well defined. You may notice that, a coset can be represented in multiple ways as long as $g_1H = g_1'H$. The question is it true that $g_1H \circ g_2H = g_1'H \circ g_2H \equiv g_1g_2 H = g_1'g_2H$? This seems hard to achieve, and indeed this is not true for most subgroups $H$. This is only true if subgroup $H$ is normal.

Definition 2.1: Normal Groups

A subgroup $H$ of group $G$ is a normal subgroup, denoted as $H \trianglelefteq G$, if $\forall g \in G$, $gHg^{-1}=H \iff gH=Hg$, i.e. left & right cosets coincide.

Definition/Lemma 2.2: Quotient Groups

Given a normal subgroup $H$ of group $G$, the quotient group, demoted as $G/H$, is the set of cosets of $H$ in $G$, with the binary operation $g_1H \circ g_2H = (g_1 g_2)H$ for $g_1, g_2 \in G$.

$Proof$. We show that given $H \trianglelefteq G$, $G/H$ is indeed a well-defined group. For $g_1, g_1', g_2 \in G$, suppose $g_1H = g_1'H$. First observe that $g_1g_2 H = g_1'g_2H \iff g_2^{-1}(g_1')^{-1}g_1g_2 H = H \iff g_2^{-1}(g_1')^{-1}g_1g_2 \in H$. Since $g_1H = g_1'H$, $(g_1')^{-1}g_1 \in H$. Thus $g_2^{-1}(g_1')^{-1}g_1g_2 \in g_2^{-1}Hg_2 = g_2^{-1}g_2H = H$. The first equality is due to the normality of $H$.

Definition 2.3: Simple Groups

A group $G$ is simple it has no proper normal subgroups.

Note that every group $G$ has trivial subgroups: $\{e\}, G$. The idea of normal and quotient groups may be intuitive if we make an analogy to integers. If we consider a group $G$ as an integer, then its normal subgroup is its divisor, and the quotient group is its quotient (and hence the name). Following this analogy, simple groups are like the prime numbers. Just like studying prime numbers is important in number theory as they are the building blocks of the number system, simple groups are like building blocks or fundamental structures. If a group is not simple, we can always “factor” it out into its normal and quotient groups, just like prime factorization.

Following this idea, we can always “project” a group to its quotient group via a homomorphism.

Definition/Lemma 2.4: Projection Homomorphism

If $H \trianglelefteq G$, the mapping $\pi: G \to G/H$ defined as $\pi(g) = gH$ is a well-defined homomorphism.

$Proof$. The mapping is well-defined since the set of cosets is a partition of $G$. It is a homomorphism since $g_1Hg_2H = g_1g_2H$ by the normality of $H$. Also note that the homomorphism is subjective.

Kernel and Image

Now we define the kernel and image of a homomorphism.

Definition 2.5: Kernel and Image

Given a homomorphism $\phi: G \to H$,

1. The kernel of $\phi$ is $Ker(\phi) = \{g \in G : \phi(g) = e_H \in H\}$.
2. The image of $\phi$ is $Im(\phi) = \{\phi(g) = g \in G\}$.

Lemma 2.6: Kernel and Image

1. The kernel of any homomorphism $\phi: G \to H$ is a normal subgroup of $G$.
2. The image of any homomorphism $\phi: G \to H$ is a subgroup of $H$.

$Proof$. It’s straightforward to check that the kernel and image are indeed subgroups of $G$ and $H$ by checking the three axioms or showing that they are closed under multiplication and inverses. Checking that the kernel is a normal subgroup is also straightforward but we will lay out the steps. We want to show that for $g \in G$, $gKer(\phi)g^{-1} = Ker(\phi)$, or for $k \in Ker(\phi), gkg^{-1} \in Ker(\phi)$. We show this by noting that $\phi(gkg^{-1}) = \phi(g)\phi(k)\phi(g^{-1}) = \phi(g)e_H\phi(g^{-1}) = e_H$.

Corollary 2.7: Kernel of Homomorphisms from Simple Groups

Given a homomorphism $\phi: G \to H$ where $G$ is a simple group, then $Ker(\phi) = H \text{ or } \{e_H\}$, i.e., $\phi$ is trivial or injective.

The First Isomorphism Theorem

Theorem 2.8: The First Isomorphism Theorem

Given a homomorphism $\phi: G \to H$, $G/Ker(\phi) \cong Im(\phi)$.

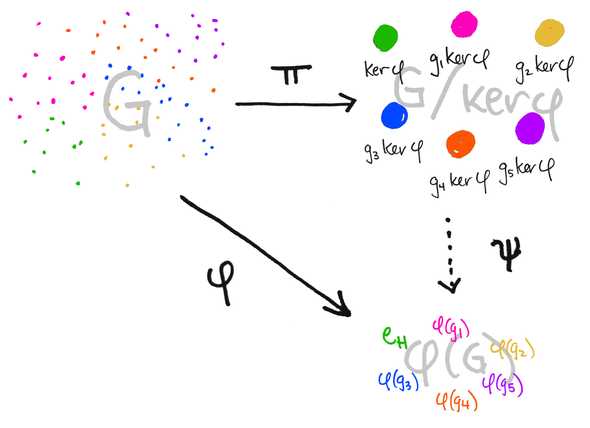
$Proof$. To prove this theorem, all we need to do is to define an isomorphism $\psi: G/Ker(\phi) \to Im(\phi)$. The idea is given the homomorphism $\phi$ and the induced projection homomorphism defined in Lemma 2.4 $\pi: G \to G/Ker(\phi)$, we define our $\psi$ so that $\phi = \psi \circ \pi$, which will complete the proof. The idea is illustrated in Figure 1.

Figure 1. The First Isomorphism Theorem. (Image source: The First Isomorphism Theorem, Intuitively. Nov. 28, 2016. Algebra, Math3ma.)

Formally, let $K$ denote $Ker(\phi)$. We define $\psi: G/K \to Im(\phi)$ by $\psi(gK) = \phi(g)$. Thus, by definition, $\phi = \psi \circ \pi$, so we only need to prove that this is a well-defined homomorphism. First, $\psi$ is well-defined since if $g_1K = g_2K$, then

$g_2g_1^{-1} \in K \iff \phi(g_2g_1^{-1}) = \phi(g_2) \phi(g_1^{-1}) = e_H \iff \phi(g_2) = \phi(g_1)$.

Second, $\psi$ is a homomorphism since

$\psi(g_1Kg_2K) = \psi(g_1g_2K) = \phi(g_1g_2) = \phi(g_1)\phi(g_2) = \psi(g_1K)\psi(g_2K)$

Thus, we proved that $\psi$ is an isomorphism.

Symmetric Groups and Alternating Groups

Upon introduction of the first isomorphism theorem, it’s convenient to introduce two kinds of very important groups.

Consider a set $S = \{1, 2, 3\}$ which contains 3 elements. We can define a bijective map $\sigma: S \to S$, which is called a permutation. For example, we can send 1 to 2, 2 to 3, 3 to 1. This permutation is denoted as $(1,2,3)$. We can also send 1 to 3 and leave 2 unchanged, and this permutation is denoted as $(1,3)$. This “parenthesized” notation is called a cycle decomposition. There are in total $3! = 6$ permutations. For a set with more elements, the cycle decomposition can be more complex. For example, for a set of $6$ elements, a permutation can be $(1, 3)(4,5,6)$. It shouldn’t be too hard to check that a k-cycle has an order $k$. More generally, a (m-cycle)(n-cycle) has an order $lcm(m,n)$. We call a 2-cycle a transposition. A cycle decomposition can always be written as composition of transpositions, for example, $(1,2,3) = (1,3)(1,2)$. In general, a m-cycle $(a_1, \cdots, a_n)$ is $(a_1, a_m)(a_1, a_{m-1})\cdots(a_1, a_2)$.

Symmetric Groups of $n$ elements $S_n$ contains all the permutations permutations on a set of $n$ elements.

Definition 2.9: Symmetric Groups $S_n$

The symmetric group on n letters, $S_n$, is a group with $n!$ elements, where the binary operation is the composition of maps.

It should be straightforward to check that this is indeed a group. It is closed by multiplication and inverse since by definition it contains all the permutations.

Definition/Lemma 2.10: Alternating Groups $A_n$

The alternating group on n letters, $A_n$, is a subgroup of $S_n$, where $A_n = \{\sigma \in S_n : \sigma \text{ is a product of even number of transpositions}\}$.

$Proof$. To justify that $A_n$ is indeed a subgroup of $S_n$, first note that the definition is unambiguous. If two products of transpositions are the same permutation, their length must have the same parity. We can first prove that the identity can only be written as the product of an even number of transpositions by induction on the length of the transpositions. This implies that two equivalent products of transpositions must have the same parity. Secondly, permutations that are products of even number of transpositions are closed under multiplication and inverses.

It may be intuitive that the size of $A_n$ is always $|S_n|/2$. However, this can be hard to prove if we don’t use techniques from group theory. By applying the first isomorphism theorem, we can prove this rather easily. To do this, we need to define another type of groups $C_n$.

Definition 2.11: Cyclic Groups $C_n$

For $n \in \mathbb Z_{\geq 1}, C_n \subset \mathbb C$, denotes the set of nth roots of unity, i.e., $C_n = \{z \in \mathbb C : z^n = 1\}$. The cyclic groups is defined as $(C_n, \times)$, where the binary operation $\times$ is the usual multplication for numbers.

You may wonder why $C_n$ have the same name as the property “cyclic”. Recall that all the cyclic groups of the same order are isomorphic, e.g., $\mathbb Z/\mathbb Z_n \cong C_n$, so in fact there are only one type of cyclic groups up to isomorphism. We just choose to use one of them for convenience.

Theorem 2.12: $[S_n : A_n] = 2$

$Proof$. To prove this claim, we want to define the subjective homomorphism $\phi: S_n \to C_2$ such that $A_n = Ker(\phi)$, and then the first isomorphism theorem gives the claim. Recall that $C_2 = \{1,-1\}. First, we define a mapping$$A: S_n \to GL(n, \mathbb Z)$$.$$GL(n,\mathbb Z)$$is a field which we haven’t introduced, but for now just understand it as a$$n\times n$$matrix over integers. We sketch the definition$$A$$with an example with$$n=3$$. For$$\sigma = (1,2,3)$$,

We define $\phi: S_n \to C_2$ as $\phi = det \circ A$. Without a proof, we claim that this is indeed a subjective homomorphism.

Proposition 2.13: Any subgroup of index 2 is normal.

Given a subgroup $H \subset G$ where $[G:H]=2$, there are only two left cosets: $H, G-H$. For a $g \in G$, if $gH = H$, then $Hg = H$ and $gH=Hg$; else if $gH = G-H$, then $Hg = G-H$ since $H$ is closed and $gH=Hg$.

Corollary 2.14: $A_n \trianglelefteq S_n$

The Second Isomorphism Theorem

Before introducing the second isomorphism theorem, we need some preparations.

Definition 2.15: Normalizer

Given a group $G$, a subset $H \subseteq G$, the normalizer of $H$ in $G$, denoted as $N_G(H)$, is $N_G(H) = \{g\in G : gHg^{-1} = H\}$.

We claim that $N_G(H)$ is a subgroup of $G$, which should be easy to check by applying definitions. Note that $H$ is a normal subgroup of $N_G(H)$. In fact, the definition of $N_G(H)$ can be phrased as the largest subgroup of $G$ in which $H$ is normal. Note also that a group $K$ is normal to $G$ iff $N_G(K) = G$.

Lemma 2.16: Product of Two Subgroups

Given two subgroups $H, K \subset G$, we define $HK = \{hk : h\in H, k\in K\}$.

1. $H\cap K$ is a subgroup of $G, H, K$;
2. $|HK| = \frac{|H||K|}{|H\cap K|}$;
3. $HK$ is a subgroup of $G$ iff $HK=KH$;
4. If $H \subset N_G(K)$, then $HK=KH$.

$Proof$. The first claim can be shown by checking the definitions. The second claim can be proven by the following steps. First, $|HK| = |\cup_{h\in H}\{hK\}| = |K||\{hK : h \in H\}|$. Second, for $h_1, h_2 \in H$,

$h_1K = h_2K \iff h_2^{-1}h_1 \in K \iff h_2^{-1}h_1 \in H \cap K \iff h_1 (H \cap K) = h_2 (H \cap K)$

so $|\{hK : h \in H\}| = |\{h(H \cap K) : h \in H\}|$. Third, using the same arguments in the proof of Lagrange’s theorem $|\{h(H \cap K) : h \in H\}| = \frac{|H|}{|H\cap K|}$.

The third claim can be shown by working from both directions, and use/check the axioms of groups. For the fourth claim, for all $h\in H$, $hKh^{-1} = K \iff hK = Kh$. Then $HK = \cup_{h\in H} hK = \cup_{h\in H} Kh = KH$.

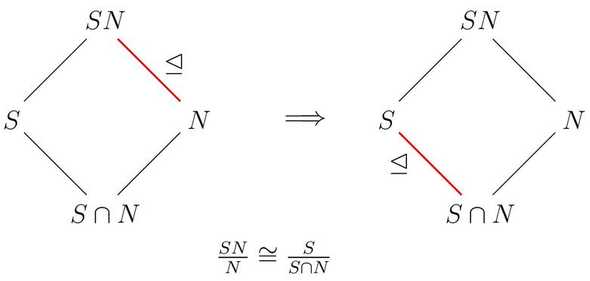
Theorem 2.17: The Second Isomorphism Theorem

Given two subgroups $H, K \subset G, H \subset N_G(K)$, then

1. $HK$ is a subgroup of $G$;
2. $K \trianglelefteq HK$;
3. $H \cap K \trianglelefteq H$;
4. $HK/K \cong H/(H \cap K)$.

Figure 2. illustrated the theorem.

Figure 2. The Second Isomorphism Theorem. (Image source: p Groups. Intuition about the second isomorphism theorem. Apr. 12, 2016. Stackexchange.)

$Proof$. For the first claim, we’ve already proven it in Lemma 2.16. For the second claim, note that $H \subset N_G(K) \implies K \trianglelefteq HK$. For the third claim, we’ve already in Lemma 2.16 that $H \cap K \trianglelefteq H$, so $H \subset N_G(K) \implies H \cap K \trianglelefteq H$. The first three claims make sure that the fourth claim is well-defined. To prove the fourth claim, we define the homomorphism $\phi: H \to HK/K$ by $\phi(h) = hK$. To complete the proof, check directly that $\phi$ is a well-defined homomorphism, $\phi$ is surjective, and that $Ker(\phi) = H \cap K$; then use the first isomorphism theorem to finish the proof.

The Third Isomorphism Theorem

Given two normal subgroups $H, K \subset G, H \subset G$, then

1. $K/H \trianglelefteq G/H$;
2. Denote $G/H$ as $\overline G$, and $K/H$ as $\overline H$, $\overline G/ \overline K \cong G/K$.

$Proof$. The second claim is a bit like canceling out factors when we are working with numbers. To prove the first claim, we directly apply the definition of normality and check. To prove the second claim, we again define a subjective homomorphism and utilize the first isomorphism theorem. We define the homomorphism $\phi: G/H \to G/K$ by $\phi(gH) = gK$. Again, we need to check that 1) $\phi$ is well-defined; 2) $\phi$ is a homomorphism; 3) $\phi$ is subjective; and 4) $Ker(\phi) = \{gH:\phi(gH)=K\} = \{gH:gK=K\} \{gH:g \in K\} = K/H$. The first three items can be shown by checking the definitions and applying the premises.

The Lattice Isomorphism Theorem

Given a normal subgroup $N \trianglelefteq G$, there exists a bijection from the set of subgroups of G that contains $N$ to the set of subgroups $\overline A = A/N$ of $G/N$. Specifically, for all subgroups $A, B \subseteq G$ such that $N \subseteq A, N \subseteq B$,

1. $A \subseteq B$ iff $\overline A \subseteq \overline B$;
2. If $A \subseteq B$, then $[B:A] = [\overline B: \overline A]$;
3. $\overline{(A \cap B)}$ = $\overline A \cap \overline B$;
4. $A \trianglelefteq B$ iff $\overline A \trianglelefteq \overline B$;

The bijection is given by some $\pi : G \to \overline G$, $\pi^{-1}(\overline A) = \{a\in A : \pi(a) = aN \in \overline A\}$, i.e. the inverse is the pre-image of $\pi$.

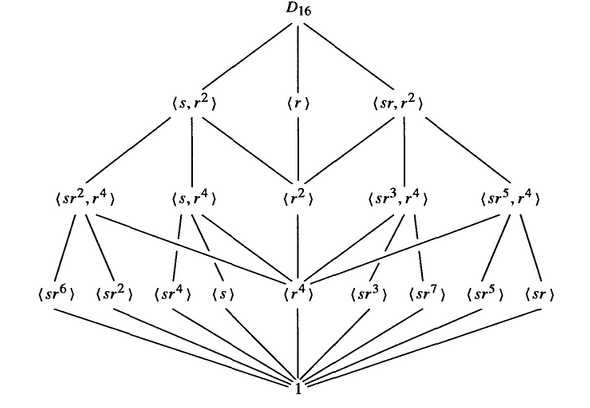
This theorem is called the lattice isomorphism theorem, since it allows us to “factor” a group into its subgroups, which is the lattice of the group, as the lattice of $D_{16}$ (dihedral groups which we haven’t defined yet) is illustrated in Figure 4.

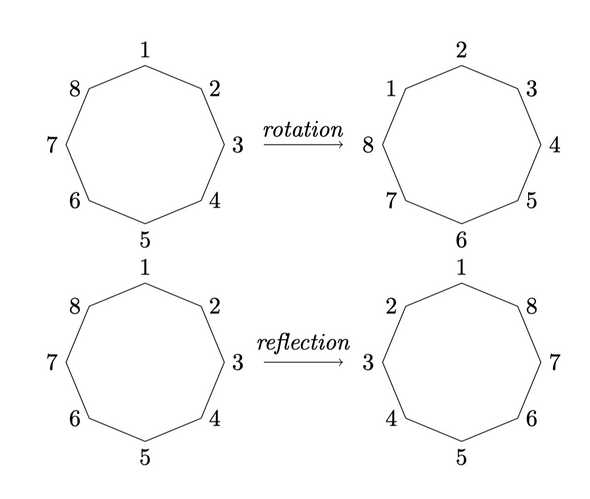
Example 2.1: Dihedral groups $D_{2n}$

Figure 3. The Generators of Dihedral groups $D_{2n}$

Dihedral groups $D_{2n}$ are subgroups of $S_n$ which consist of the rigid motions (reflections and rotations) of a regular n-sided polygon or n-gon. It should take some pondering, but there are exactly $2n$ unique motions, further every motion can be generated by the reflection and the $2\pi/n$ rotation. Say the reflection is $s$ and the rotations is $r$, then formally,

$D_{2n} = \langle r, s \mid r^{2n} = s^2 = e, rsr = s \rangle$

Figure 4. The Lattice of $D_{16}$.

References

[1] Siegel, Kyler. MATH GU4041 Introduction to Modern Algebra I. Department of Mathematics, Columbia University. 2019.

[2] Dummit, David and Foote, Richard. Abstract Algebra. Third Edition. John Wiley and Sons, Inc. 2004.