This post gives a gentle introduction to Task and Motion Planning (TAMP).

Motivation and Introduction

Task and Motion Planning (TAMP) concerns long-horizon planning planning for a robot. It comes at the intersection of motion planning and task planning, as the name suggests. Motion planning problems require a simple high-level plan (pick up the package) but complex low-level actions (avoid collisions during the pick-up); task planning problems require a complex high-level plan, e.g., a step-by-step procesure for reversing a Rubik’s cube, but the low-level actions are assumed to be simple. However, real-world problems oftren require both a complex high-level plan and each step requires complex motion planning. Moreover, it’s not as simple as creating a high-level plan using task planning, and then optimize for low-level actions using motion planning, as the problems are interleaved. For example, if the robot wants to pick up a package that is under other objects, then the high-level plan needs to first move away the other objects. This is a typical situation when the high-level plan needs to consider the low-level geometry of the problem. Task and motion planning concerns these complex long-horizon problems.

Background

Motion Planning

Motion planning can be seen as a search problem in the configuration space $Q$ with constraints. Given an initial configuration $q_0 \in Q$, a subset of goal states $Q^* \subset Q$. The constraints specfied as a function $F: Q \rightarrow \{0, 1\}$, where $F(q)=1$ suggests feasible configuration, and it induces a feasible subspace $Q_F = \{q \in Q: F(q)=1\}$. The solution of the motion planning problem is a continuous “path”. We specify the path with a continuous function $\tau: [0,1] \rightarrow Q_F$, where the path starts at the initial configuration, i.e. $\tau(0)=q_0$, and ends at a goal configuration, i.e. $\tau(1) \in Q_F$.

Multi-Model Motion Planning (MMMP)

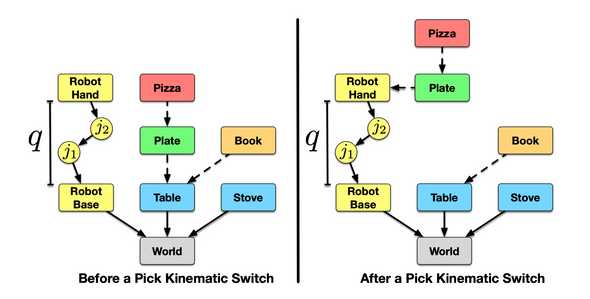
The motion planning formulation we’ve talked about is limited to a single “mode”. If the kinematics of the system changes (the mode switches), then the system specfies a different configuration space and constraint function. For example, when the robot picks up an object, its movement will be further constrained by the geometry of the object. To abstractly desribe a mode, we can use the concept of a kinematic graph. In a kinematic graph, a vertex represents an object, a robot body, or a robot joint, and a directed edge represents the relative pose of the child relative to the parent. A mode can then be specified by the discrete structure encoded in a kinematic graph and the continuous values of the transformations specified by the edges.

Now to further abstract the representations, we introduce the concept of mode family. Loosely speaking, a mode family describes a robot status. For example, in pick-and-place task, when the robot’s gripper is free, we have the mode family of free motion; when the robot picks up an object, we have the mode family of transfer. We denote a mode family with $\Sigma$, and a mode is a mode family parametrized with $\sigma = \Sigma(\theta)$ (e.g., specifying the transformations on the edges of the kinematic grpah) with an associated constraint function $F_\sigma$.

The solution of the MMMP is a trajectory of tuples $(\sigma_i, \tau_i)$, where $\sigma_i$ is a mode, and $\tau_i$ is a path constrained to the mode $\sigma_i$, i.e. $\tau_i(t) \in Q_{F_{\sigma_i}}$. Further, the path admits a “mode switch”, i.e., $\tau_i(1) \in Q_{F_{\sigma_{i+1}}}$.

Task Planning

Task planning can be seen a search problem in the abstracted space. Given a state space $\mathcal S$, the transition function $\tau \in \mathcal S \times \mathcal S$, a start state $s_0 \in \mathcal S$, and goal states $S^* \subset \mathcal S$, the goal is to find a sequence of actions from action space $\mathcal A$ that transition from $s_0$ to a state in $S^*$. Task planning abstracts both the state space and the action space to efficiently search a task plan.

To abstract the state space, we make use of predicates. Each predicate is a function that takes as inputs the current world state and a set of objects and outputs a set of “state variables”, e.g. if the robot is holding the book, isHolding(book) =True, Holding()=book. In particular, isHolding is the predicate, and isHolding(?object) is lifted (with a placeholder), while isHolding(book) is grounded. The predicates are usually hand-crafted. A set of predicates induces an abstract state space, where each state can be represented as a set of state variables. For example, if we have two objects book and pencil and two lifted predicates Holding() and isHolding(?object), then an abstract state is {Holding=book, isHolding(book)=True, isHolding(pencil)=False}. (Of course, here isHolding and Holding are repetitive.)

To abstract the action space, we make use of operators. An operator has pre-conditions (pre) and effects (eff). If the pre-conditions are satisfied, it can be executed to obtain the effects. Below are some example operators: moveF refers to moving the robot when it’s free, and moveH refers to moving the robot when it’s holding an object (different modes as we discussed).

The solution of a task planning problem is then a sequence of operators that achieves a (abstract) goal state. For example, to cook and serve a frozen pizza, a plan is as follows:

π = {moveF[Table,Box], pick[Pizza], moveH[Box,Oven], place[Pizza], cook[Pizza], pick[Pizza], moveH[Oven,Plate], place[Pizza]}

Task and Motion Planning (TAMP)

A TAMP problem can be seen as a MMMP problem with variables that are not geometric or kinematic, or task planning problem with continuous parameters and constraints. The operators in TAMP can enhanced with constraints that need to be satisfied for motion planning. For example, moveWithin moves the robot within a mode, and switchModes switch between modes. Note that we now have constraints for motion planning. For example, the pick action has the constraint $Kin[obj](q, p, g)$, which is a kinematic constraint saying that for an object obj, if the robot is in configuration q and holding obj in grasp g, then obj will be at pose p. In moveF and moveH, the $Motion(q, \tau, q')$ constraint specifies the relationship between a trajectory $\tau$ and two robot configurations, asserting that $\tau(0) = q, \tau(1) = q′$ and that $\tau$ is continuous. Notice that the trajectory $\tau$ appears neither in the preconditions nor effects of these actions; they are auxiliary parameters that describe motion within the modes. The collision-free constraint $CFreeA[obj](p, g, τ)$ asserts that if object $A$ is at pose $p,$ the robot is holding obj in grasp $g$, and it executes trajectory $\tau$, no collision will occur. The constraint $CFreeW[obj](g, τ)$ is defined similarly except that it involves the fixed objects in the world.

The solution of the problem is a plan skeleton with some free parameters that need to be solved with motion planning. For example, to cook a pizza, the solution may be:

$[moveF(q_0 , τ_1 , q_1 ), pick[A](q_1 , p_0 , g_2 ), moveH[A](q_1 , τ_3 , q_3 ), place[A](q_3 , p_4 , g_2 ), cook[A](p_4)]$

where $q_1, τ_1, g_2, q_2, τ_3, p_4$ are the free parameters.

Learning for TAMP

Assumptions of Classical TAMP

The most basic TAMP makes several assumptions about the task to simplify the problem.

• The state of the world is completely known. Further, we have

  • (1) object-centric descriptions of states, e.g., the pose and attributes of each object, and
  • (2) an abstraction of the world through a set of predicates that are hand-crafted.
• The transition function of the world is known, which means that we know the effects of an action.
• The skills are hand-crafted. Each skill consists of an operator and a policy. An operator, as mentioned, has constraints, pre-conditions, and effects. An operator is an action in the high-level (abstracted) space. A policy outputs low-level actions that achieve the intended effects of an operator. (In some literature, a skill also consists of a sampler that outputs sub-goals (low-level states) given an operator, and a policy is conditioned on sub-goals instead.)
• The goal is specified with a set of grounded predicates.

Learning Algorithms and TAMP

With the advancement in learning methods, we can instead learn these assumed components from demonstration data. Moreover, TAMP may be integrated with reinforcement learning (RL) and large language models (LLMs)for planning in addition to tranditional AI planning algorithms. Here we introduce some relevant ideas and works.

• Learning Assumed Components

  • learning to represent the state of the world with SoTA perception models
  • learning the transition function (the world dynamics) with RL

• Learning Hand-Crafted Components

  • learning predicates from demonstration data
  • learning operators from demonstration data
  • learning policies with imitation learning / RL

• Learning/Planning with LLMs

  • Generate symbolic states with visual-language models
  • Creating symbolic plans with LLMs

References

[1] Garrett, Caelan Reed, et al. “Integrated task and motion planning.” Annual review of control, robotics, and autonomous systems 4 (2021): 265-293.

[2] Silver, Tom, et al. “Learning symbolic operators for task and motion planning.” 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2021.

[3] Chitnis, Rohan, et al. “Learning neuro-symbolic relational transition models for bilevel planning.” 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2022.

[4] Silver, Tom, et al. “Learning neuro-symbolic skills for bilevel planning.” arXiv preprint arXiv:2206.10680 (2022).

[5] Silver, Tom, et al. “Inventing relational state and action abstractions for effective and efficient bilevel planning.” arXiv preprint arXiv:2203.09634 (2022).

[6] Ding, Yan, et al. “Task and Motion Planning with Large Language Models for Object Rearrangement.” arXiv preprint arXiv:2303.06247 (2023).

[7] Lin, Kevin, et al. “Text2Motion: From Natural Language Instructions to Feasible Plans.” arXiv preprint arXiv:2303.12153 (2023).

[8] Agia, Christopher, et al. “STAP: Sequencing Task-Agnostic Policies.” arXiv preprint arXiv:2210.12250 (2022).