This is the first post of the Introduction to Quantum Mechanics series. In the first post, we introduce the Stern-Gerlach experiment, which leads to the discovery of spin, a fundamental quantum mechanical nature of elementary particles. We then lay out the postulates of the QM. Finally, we introduce the Dirac notation, the mathematical notation we used in QM.

The Stern-Gerlach Experiment

The Stern-Gerlach Experiment is the decisive experiment to demonstrate the angular momentum quantization of elementary particles. We start the discussion with a magnetic dipole moment.

A magnetic dipole moment $\pmb{\mu}$ in an externally produced magnetic field $\pmb{B}$ has a potential energy

If the magnetic field is non-uniform, the magnetic dipole moment experiences a force proportional to the gradient of the magnetic field:

If the electron with is visualized as a classical charged particle rotating about an axis with angular momentum $\pmb L$, the electron’s magnetic dipole moment is:

In general, for a charged point particle with charge $q$, mass $m$, and angular momentum $\pmb L$ has the dipole moment:

Besides the orbital angular momentum $\pmb L$, a particle also has intrinsic angular momentum, or spin, $\pmb{S}$. To intuitively (but incorrectly) understand spin: the Earth orbits around the Sun and has the orbital angular momentum, and it also orbits about its axis and has the intrinsic angular momentum. For now, we can understand it as a form of angular momentum. The magnetic dipole moment of a charged particle due to its spin is:

which has a $g$ factor experimentally determined for different particles. For example, $g=2.00$ for electrons.

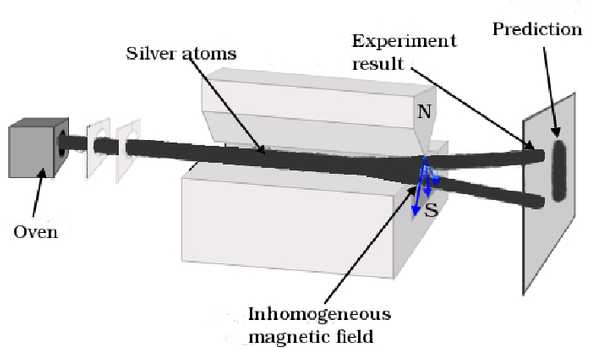
Figure 1. The Stern-Gerlach Experiment’s Setup. (Image source: Tanrıverdi, V. (2015). Stern-Gerlach Experiment and Spin. viXra.)

Now we’re ready to describe the Stern-Gerlach experiment as shown in Figure 1. Heated silver atoms are shot from an over and pass through an inhomogeneous magnetic field produced by a pair of magnets. Let the direction in which the inhomogeneous magnetic field’s gradient is the largest the $z$ direction, the force experienced by a silver atom in the $z$ direction is:

where $\theta$ is the angle between the magnetic moment’s orientation and $z$ direction.

Silver atoms have 47 electrons. Atomic theory tells us that 46 of the electrons have a zero net angular momentum due to cancellation and do not contribute to the magnetic dipole, and the 47th electron has a zero angular momentum. Moreover, the magnetic dipole of the nucleus can be neglected because its mass is significantly larger than the electrons. Therefore, the force experienced by the silver atom is effectively determined by the spin of an electron.

Considering $|\pmb \mu|$ and $|\pmb S|$ as constants for electrons, the experimenters expected $\mu_z$ of the electron to take a continuum of values ranging from $+|\pmb \mu|$ to $-|\pmb \mu|$ due to different orientations $\theta$. According to this prediction, the projections of the silver atoms onto a detector will result in a continuum of displacements. However, the silver atoms take only two displacements, and $\mu_z$ takes only two values, corresponding to $\pm \hbar/2$ for $S_z$.

The result should be rather bizarre if you’re not familiar with quantum mechanics. The $z$ direction we picked is completely arbitrary! It feels like that when the electron passes through the inhomogeneous magnetic field, it suddenly orients itself along the direction with the largest gradient, which cannot be explained by classical mechanics. The following experiments maybe even more confusing, but they will also give us more insights into quantum mechanics.

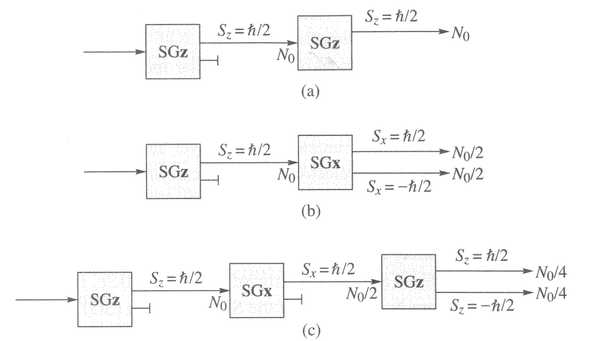
Figure 2. The Follow-up on Stern-Gerlach Experiment. (Image source: Townsend, John. A Modern Approach to Quantum Mechanics. 2nd Edition.)

In experiment (a), we add a second inhomogeneous magnetic field oriented in the same $z$ direction after picking out electrons with $\mu_z = + \hbar/2$. We get the same number of electrons with $\mu_z = + \hbar/2$.

In experiment (b), we add a second inhomogeneous magnetic field oriented in an orthogonal direction which we call $x$ after picking out electrons with $\mu_z = + \hbar/2$. We get a even split of electrons with $\mu_x = \pm \hbar/2$. This seems to be quite overwhelming, as it suggests that $\mu_x$ and $\mu_z$ are independent.

In experiment (c), we add a third inhomogeneous magnetic field oriented in $z$ direction after picking out electrons with $\mu_z = + \hbar/2$ from the first field and electrons with $\mu_x = + \hbar/2$ in the second field. We get a even split of electrons with $\mu_z = \pm \hbar/2$. $\mu_z$ becomes totally unrelated to the original electrons after passing the second field!

The Postulates of Quantum Mechanics

To explain these results, classical mechanics is of no good. We now need a new system of mechanics, a new worldview, and we start with the postulates.

1. The state of a quantum mechanical system is specified by a wave function as a function of positional coordinates and time $\Psi(\pmb r, t)$.

   The set of all possible normalizable wave functions of a system with a particular choice of basis form a Hilbert Space, an infinitely dimensional function space. Therefore, a quantum mechanical state can be represented by a vector (a function is an infinite-dimension vector) in the Hilbert Space.

   Mathematically, we can calculate the inner product of the two functions in the Hilbert space:

   $$\int^\infty_{-\infty} \psi^* (\pmb r, t) \Psi(\pmb r, t) d\tau$$

   Mathematically, the inner product of a normalized vector onto itself is 1, i.e.

   $$\int^\infty_{-\infty} \Psi^* (\pmb r, t) \Psi(\pmb r, t) d\tau = \int^\infty_{-\infty} | \Psi(\pmb r, t) |^2 d\tau = 1$$

   This also has important physical significance, as

   $$\Psi^* (\pmb r, t) \Psi(\pmb r, t) d\tau =| \Psi(\pmb r, t) |^2 d\tau$$

   is the probability that the particle lies in the volume element $d\tau$, and the probability of the particle being in the whole space should be 1.

   $\Psi(\pmb r, t)$ is the probability amplitude, and its modulus square $| \Psi(\pmb r, t) |^2$ is the probability density.

   More generally, a quantum mechanical state may use the set of basis other than positional coordinates and time: it can also be written as a function of other variables. Suppose the wave function $\Psi(\pmb x)$ is as a function of $\pmb x$. $\Psi(\pmb x)$ is the probability amplitude and $| \Psi(\pmb x) |^2$ is the probability density to measure the particle in the basis states $\pmb x$.

   To ease the notations in quantum mechanics, we use Dirac notation or bra-ket notation. In this notation, a quantum mechanical state is represented by a ket, $|\Psi\rangle$, and its conjugate is represented by a bra, $\langle\Psi|$. The expression $\langle\psi|\Psi\rangle$ denotes the inner product of two states. We express the wave function $\Psi(\pmb r, t)$ as $\langle\pmb r, t|\Psi\rangle$ and its conjugate $\Psi^* (\pmb r, t)$ as $\langle\Psi|\pmb r, t\rangle$. We have the probability density

   $$|\langle\pmb r, t|\Psi\rangle|^2 = \langle\Psi|\pmb r, t\rangle \langle\pmb r, t|\Psi\rangle$$

   More generally, for a set of basis states $|\pmb x \rangle$, we have the probability density

   $$|\langle\pmb x|\Psi\rangle|^2 = \langle\Psi|\pmb x\rangle \langle\pmb x|\Psi\rangle$$

   For a finite dimensional space, $|\langle\pmb x = x|\Psi\rangle|^2$ gives the probability for the particle to be in the state $x$.

   For a finite dimensional space, we can also represent states with vector representations. Assume a 2-dimensional space with normalized basis states
   $|+z\rangle$ and $|-z\rangle$, i.e.

   $$\langle+z|-z\rangle = \langle-z|+z\rangle = 0$$ $$\langle+z|+z\rangle = \langle-z|-z\rangle = 1$$

   States $|\psi\rangle$ and $|\psi\rangle$ in the space can be represented by

   $$|\psi\rangle = a |+z\rangle + b |-z\rangle \equiv \begin{pmatrix} a \\ b \end{pmatrix}$$ $$|\psi\rangle = c |+z\rangle + d |-z\rangle \equiv \begin{pmatrix} c \\ d \end{pmatrix}$$

   Their conjugates are

   $$\langle\psi| = \langle+z|a^* + \langle-z|b^* \equiv \begin{pmatrix} a^* & b^* \end{pmatrix}$$ $$\langle\psi| = \langle+z|c^* + \langle-z|d^* \equiv \begin{pmatrix} c^* & d^* \end{pmatrix}$$

   and the inner product of the two states is:

   $$\begin{aligned} \langle\psi|\psi\rangle &= (\langle+z|a^* + \langle-z|b^* ) (c |+z\rangle + d |-z\rangle) \\ &= a^* b + c^* d \\ &= \begin{pmatrix} a^* & b^* \end{pmatrix} \begin{pmatrix} c \\ d \end{pmatrix} \end{aligned}$$

2. To every observable in classical mechanics, there corresponds a linear, Hermitian operator in quantum mechanics.

   An quantum mechanical operator $\hat O$ transforms a quantum mechanical state:

   $$|\psi\rangle = \hat O |\psi\rangle$$

   Each operator $\hat O$ has an adjoint operator $\hat O ^\dagger$. Without attending to mathematical formalism, an operator $\hat O$ acts on a ket while its adjoint $\hat O ^\dagger$ acts on the corresponding bra.

   $$\langle\psi| = \hat O^\dagger \langle\psi|$$

   In a finite dimension space, just as a state can be represented by a vector, an operator can be represented by a matrix. The adjoint of the operator $\hat O ^\dagger$ in this case is the transpose conjugate of $\hat O$.

   An operator is Hermitian if its adjoint is itself, or it is self-adjoint. In a finite-dimensional space, a Hermitian operator is a real symmetric matrix. Hermitian operators have several important properties, which we will layout after the following postulates.

3. In any measurement of the observable associated with operator $\hat{A}$, the only values that will be observed are its eigenvalues $a$.

   This postulate mandates the measurements to be quantized (except an operator has a continuum of eigenvalues). Boilers alert: the spin-1/2 operator has only two eigenvalues, and we can only observe two possible values for the electron spin.

4. If a system is in a state described by a normalized wave function $\Psi$, then the average value of the observable corresponding to $\hat{A}$ is given by

   $$<A> = \int_{-\infty}^{\infty} \Psi^{* } \hat{A} \Psi d\tau \equiv \langle\Psi|\hat{A}|\Psi\rangle$$

   The latter expression is the Dirac notation of expectation.

   The 2nd, 3rd, and 4th postulates are related by the properties of a Hermitian operator (proofs):

   • a. Hermitian operators have real eigenvalues: we cannot obtain complex measurements.
   • b. Hermitian operators have orthogonal eigenvectors: an eigenvector is the state of a particle upon measurement, and it cannot have more than one state.
   • c. Hermitian operators have real expectation values: we cannot obtain complex expectations of measurements.
   • d. Hermitian operators have eigenvectors that span the Hilbert space.

5. The wave function or state function of a system evolves in time according to the time-dependent Schrödinger equation

   $$\hat{H} \Psi({\bf r}, t) = i \hbar \frac{\partial \Psi}{\partial t}$$

   This will be discussed in a later post, but come on, you must have heard of it.

6. The total wave function must be antisymmetric with respect to the interchange of all coordinates of one fermion with those of another. The electronic spin must be included in this set of coordinates.

   This will be discussed in an even later post.

Back to the Stern-Gerlach Experiment

When we experiment with a Stern-Gerlach device oriented in the z-direction device, we are effectively measuring the spin of the electrons in the z-direction. According to the postulates, we have a Hermitian operator $\hat{S_z}$, and the experimental results show that $\hat{S_z}$ has two eigenvalues $\pm \hbar/2$. We call the corresponding eigenvectors $|\pm z\rangle$, i.e.

In matrix representation, we have

By setting up a Stern-Gerlach device oriented in the x-direction, we find out the two eigenvalues $\pm \hbar/2$ of $\hat{S_x}$. We call the corresponding eigenvectors $|\pm x\rangle$. Since we know $|\pm z\rangle$ spans the Hilbert space, $|\pm x\rangle$ must be a superposition of $|\pm z\rangle$.

In the basis of $|\pm z\rangle$, the coordinate representation of $|\pm x\rangle$ is

In experiment (c), when we measure of $S_z$, we get a probability distribution of measurements: one-half of the particles has $S_z = +\hbar/2$ and therefore eigenstate $|+ z\rangle$, and the other half has $S_z = -\hbar/2$ and therefore eigenstate $|- z\rangle$. (This also means that we cannot obtain the measurements of $S_x$ and $S_z$ at the same time, the first suggestion to the uncertainty principle.) To find out the representation of $|+ x\rangle$, we set up the two equations of the probability density

By solving the equations, we get:

where $\delta_a$ and $\delta_b$ are real complex phases. We will find out in the next post that

You can use this result to verify the results of the experiment (b).

References

[1] Zajc, William. PHYS GU4021-4022 Quantum Mechanics I-II, Department of Physics, Columbia University. 2019-2020.

[2] Townsend, John. A Modern Approach to Quantum Mechanics. 2nd Edition.

[3] Sherrill, David. “Postulates of Quantum Mechanics.” A Brief Review of Elementary Quantum Chemistry, School of Chemistry and Biochemistry, Georgia Institute of Technology.